what tangential impulse must be given to the body to escape to infinity

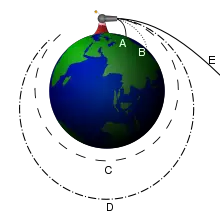
Isaac Newton's analysis of escape velocity. Projectiles A and B fall back to earth. Projectile C achieves a circular orbit, D an elliptical i. Projectile E escapes.

In physics, escape velocity is the speed of an object at which its kinetic energy is equal to the magnitude of its gravitational potential free energy, equally calculated past the equation ${\displaystyle U_{thou}=-Gm_{one}m_{2}/r}$ . It is usually described equally the speed needed to "interruption complimentary" from a gravitational field (without any additional impulse). The term escape velocity really refers to a speed rather than a velocity—that is, it specifies how fast the object must motility, only the direction of movement is irrelevant. In more technical terms, escape velocity is a scalar (not a vector) quantity.

Contents

• 1 Overview
• two Misconceptions
• 3 Orbit
• four List of escape velocities
• five Calculating escape velocity
• six Deriving escape velocity using calculus
  • six.ane Derivation using only g and r
  • half dozen.2 Derivation using M and M
  • half-dozen.3 The derivations are consistent
• vii Multiple sources
• 8 Gravity well
• ix Meet as well
• x Notes
• 11 References
• 12 External links
• 13 Credits

Overview

The phenomenon of escape velocity is a effect of conservation of energy. For an object with a given total free energy, which is moving subject field to conservative forces (such every bit a static gravity fields) the object tin can reach only combinations of places and speeds which have that total energy; and places which have a higher potential energy than this cannot be reached at all.

For a given gravitational potential energy at a given position, the escape velocity is the minimum speed an object without propulsion needs to take sufficient energy to be able to "escape" from the gravity, that is, so that gravity will never manage to pull it back. For the sake of simplicity, unless stated otherwise, this commodity will presume that the scenario one is dealing with is that an object is attempting to escape from a uniform spherical planet past moving straight upwards (along a radial line away from the center of the planet), and that the just meaning strength acting on the moving object is the planet's gravity.

Escape velocity is actually a speed (not a velocity) because it does not specify a management: no matter what the direction of travel is, the object can escape the gravitational field. The simplest way of deriving the formula for escape velocity is to use conservation of energy. Imagine that a spaceship of mass m is at a distance r from the eye of mass of the planet, whose mass is M. Its initial speed is equal to its escape velocity, ${\displaystyle v_{e}}$ . At its concluding land, it will be an infinite distance away from the planet, and its speed volition exist negligibly small and assumed to be 0. Kinetic energy G and gravitational potential energy U _g are the only types of free energy that we will deal with, and then by the conservation of energy,

${\displaystyle (K+U_{g})_{i}=(Chiliad+U_{1000})_{f}.\,}$

K _f = 0 because final velocity is zero, and U _gf = 0 because its last distance is infinity, then

${\displaystyle {\frac {1}{2}}mv_{e}^{2}+{\frac {-GMm}{r}}=0+0}$

${\displaystyle v_{e}={\sqrt {\frac {2GM}{r}}}}$

Defined a little more than formally, "escape velocity" is the initial speed required to become from an initial point in a gravitational potential field to infinity with a residual velocity of nil, with all speeds and velocities measured with respect to the field. Additionally, the escape velocity at a point in space is equal to the speed that an object would have if it started at rest from an infinite distance and was pulled by gravity to that signal. In common usage, the initial point is on the surface of a planet or moon. On the surface of the World, the escape velocity is about eleven.2 kilometers per second (~6.96 mi/due south), which is approximately 34 times the speed of sound (mach 34) and at least 10 times the speed of a rifle bullet. However, at 9,000 km distance in "space," it is slightly less than vii.1 km/southward.

The escape velocity relative to the surface of a rotating body depends on management in which the escaping torso travels. For case, every bit the World's rotational velocity is 465 k/s at the equator, a rocket launched tangentially from the Globe's equator to the eastward requires an initial velocity of about 10.735 km/s relative to Earth to escape whereas a rocket launched tangentially from the Earth's equator to the west requires an initial velocity of about xi.665 km/s relative to Earth. The surface velocity decreases with the cosine of the geographic latitude, so space launch facilities are often located as close to the equator as viable, for example, the American Cape Canaveral (latitude 28°28' Due north) and the French Guiana Space Heart (latitude 5°xiv' N).

Escape velocity is independent of the mass of the escaping object. It does not matter if the mass is ane kg or grand kg, escape velocity from the aforementioned point in the same gravitational field is always the same. What differs is the amount of energy needed to accelerate the mass to reach escape velocity: The energy needed for an object of mass ${\displaystyle m}$ to escape the Earth'southward gravitational field is GMm / r, a role of the object's mass (where r is the radius of the Earth, 1000 is the gravitational constant, and Thousand is the mass of the Earth). More massive objects crave more energy to reach escape velocity. All of this, of course, assumes i is neglecting air resistance.

Misconceptions

Planetary or lunar escape velocity is sometimes misunderstood to be the speed a powered vehicle (such as a rocket) must reach to exit orbit; however, this is not the case, every bit the quoted number is typically the surface escape velocity, and vehicles never achieve that speed direct from the surface. This surface escape velocity is the speed required for an object to leave the planet if the object is only projected from the surface of the planet and and then left without whatsoever more kinetic energy input: In practice the vehicle's propulsion system will continue to provide energy after information technology has left the surface.

In fact a vehicle can go out the Earth's gravity at whatsoever speed. At college distance, the local escape velocity is lower. But at the instant the propulsion stops, the vehicle tin can only escape if its speed is greater than or equal to the local escape velocity at that position. At sufficiently high distance this speed can approach 0.

Orbit

If an object attains escape velocity, but is not directed straight away from the planet, then information technology will follow a curved path. Even though this path volition not course a closed shape, it is still considered an orbit. Assuming that gravity is the only significant force in the system, this object'due south speed at any point in the orbit will be equal to the escape velocity at that indicate (due to the conservation of energy, its full energy must always exist 0, which implies that information technology always has escape velocity; see the derivation higher up). The shape of the orbit will exist a parabola whose focus is located at the centre of mass of the planet. An bodily escape requires of course that the orbit non intersect the planet, since this would cause the object to crash. When moving abroad from the source, this path is called an escape orbit; when moving closer to the source, a capture orbit. Both are known as C3 = 0 orbits (where C3 = - μ/a, and a is the semi-major centrality).

Remember that in reality at that place are many gravitating bodies in space, so that, for instance, a rocket that travels at escape velocity from Earth will not escape to an space distance away because it needs an even higher speed to escape the Sun'southward gravity. In other words, near the World, the rocket's orbit will appear parabolic, but eventually its orbit volition become an ellipse around the Lord's day.

Listing of escape velocities

To exit planet Earth an escape velocity of eleven.2 km/s is required, however a speed of 42.1 km/s is required to escape the Sun'due south gravity (and go out the solar system) from the same position

Location	with respect to	Ve [1]		Location	with respect to	Vdue east [ane]
on the Lord's day,	the Sun's gravity:	617.five km/s
on Mercury,	Mercury's gravity:	iv.4 km/s		at Mercury,	the Lord's day's gravity:	67.7 km/s
on Venus,	Venus' gravity:	10.4 km/southward		at Venus,	the Sun's gravity:	49.v km/s
on Earth,	the Earth's gravity:	11.two km/s		at the Earth/Moon,	the Sun's gravity:	42.1 km/south
on the Moon,	the Moon's gravity:	2.4 km/s		at the Moon,	the World's gravity:	1.four km/s
on Mars,	Mars' gravity:	five.0 km/due south		at Mars,	the Dominicus'south gravity:	34.1 km/south
on Jupiter,	Jupiter's gravity:	59.5 km/s		at Jupiter,	the Sun's gravity:	18.5 km/southward
on Saturn,	Saturn's gravity:	35.5 km/south		at Saturn,	the Sun's gravity:	13.half-dozen km/southward
on Uranus,	Uranus' gravity:	21.3 km/s		at Uranus,	the Lord's day's gravity:	9.half dozen km/south
on Neptune,	Neptune'due south gravity:	23.5 km/s		at Neptune,	the Sun's gravity:	seven.7 km/s
in the solar system,	the Milky way'southward gravity:	~1,000 km/s

Because of the atmosphere it is non useful and hardly possible to give an object near the surface of the Earth a speed of eleven.2 km/s, as these speeds are too far in the hypersonic regime for most practical propulsion systems and would crusade nearly objects to burn up due to atmospheric friction. For an actual escape orbit a spacecraft is first placed in depression World orbit and and so accelerated to the escape velocity at that altitude, which is a fiddling less—well-nigh ten.9 km/s. The required dispatch, however, is mostly even less because from that sort of an orbit the spacecraft already has a speed of viii km/southward.

Calculating escape velocity

To expand upon the derivation given in the Overview,

${\displaystyle v_{e}={\sqrt {\frac {2GM}{r}}}={\sqrt {\frac {2\mu }{r}}}={\sqrt {2gr\,}}.}$

where ${\displaystyle v_{east}}$ is the escape velocity, G is the gravitational constant, Thousand is the mass of the body existence escaped from, chiliad is the mass of the escaping body, r is the altitude between the heart of the body and the point at which escape velocity is being calculated, g is the gravitational acceleration at that distance, and μ is the standard gravitational parameter.^[2]

The escape velocity at a given superlative is ${\displaystyle {\sqrt {2}}}$ times the speed in a circular orbit at the aforementioned summit (compare this with equation (fourteen) in round motion). This corresponds to the fact that the potential free energy with respect to infinity of an object in such an orbit is minus two times its kinetic free energy, while to escape the sum of potential and kinetic energy needs to be at to the lowest degree zero.

For a body with a spherically-symmetric distribution of mass, the escape velocity ${\displaystyle v_{e}}$ from the surface (in m/south) is approximately two.364×10⁻⁵ m^one.vkg^−0.5due south⁻¹ times the radius r (in meters) times the foursquare root of the average density ρ (in kg/one thousand³), or:

${\displaystyle v_{e}\approx two.364\times 10^{-v}r{\sqrt {\rho }}.\,}$

Deriving escape velocity using calculus

These derivations use calculus, Newton'southward laws of motion and Newton'due south constabulary of universal gravitation.

Derivation using only g and r

The World's escape speed can be derived from "g," the acceleration due to gravity at the Earth's surface. Information technology is not necessary to know the gravitational constant G or the mass M of the Globe. Permit

r = the Earth's radius, and

g = the acceleration of gravity at the Earth's surface.

To a higher place the Earth'southward surface, the dispatch of gravity is governed past Newton's inverse-square police force of universal gravitation. Accordingly, the acceleration of gravity at acme s above the center of the World (where southward > r ) is ${\displaystyle g(r/s)^{2}}$ . The weight of an object of mass k at the surface is g m, and its weight at height s above the heart of the World is gm (r / s)². Consequently the energy needed to elevator an object of mass g from height southward above the World's center to height due south + ds (where ds is an infinitesimal increment of s) is gm (r / s)² ds. Since this decreases sufficiently fast as s increases, the full energy needed to lift the object to infinite peak does not diverge to infinity, but converges to a finite amount. That amount is the integral of the expression above:

${\displaystyle \int _{r}^{\infty }gm(r/s)^{two}\,ds=gmr^{2}\int _{r}^{\infty }s^{-2}\,ds=gmr^{2}\left[-s^{-ane}\right]_{south:=r}^{southward:=\infty }}$

${\displaystyle =gmr^{ii}\left(0-(-r^{-i})\right)=gmr.}$

That is how much kinetic energy the object of mass 1000 needs in order to escape. The kinetic energy of an object of mass m moving at speed v is (1/2)mv². Thus we need

${\displaystyle {\brainstorm{matrix}{\frac {one}{ii}}\end{matrix}}mv^{2}=gmr.}$

The cistron m cancels out, and solving for v nosotros become

${\displaystyle 5={\sqrt {2gr\,}}.}$

If we take the radius of the Globe to be r = 6400 kilometers and the dispatch of gravity at the surface to exist g = 9.8 k/s², nosotros get

${\displaystyle v\cong {\sqrt {2\left(9.eight\ {\mathrm {1000} /\mathrm {s} ^{2}}\right)(vi.4\times x^{six}\ \mathrm {yard} )}}=11\,201\ \mathrm {m} /\mathrm {southward} .}$

This is just a bit over 11 kilometers per 2nd, or a scrap under 7 miles per second, as Isaac Newton calculated.

Derivation using Grand and M

Let G be the gravitational constant and let One thousand be the mass of the earth or other body to be escaped.

${\displaystyle ma=m{\frac {dv}{dt}}=-{\frac {GMm}{r^{2}}}\,}$

${\displaystyle a={\frac {dv}{dt}}=-{\frac {GM}{r^{2}}}\,}$

By applying the chain rule, ane gets:

${\displaystyle {\frac {dv}{dt}}={\frac {dv}{dr}}\cdot {\frac {dr}{dt}}=-{\frac {GM}{r^{2}}}\,}$

Because ${\displaystyle v={\frac {dr}{dt}}}$

${\displaystyle {\frac {dv}{dr}}\cdot v=-{\frac {GM}{r^{two}}}\,}$

${\displaystyle v\cdot dv=-{\frac {GM}{r^{2}}}\,dr\,}$

${\displaystyle \int _{v_{0}}^{five(t)}v\,dv=-\int _{r_{0}}^{r(t)}{\frac {GM}{r^{2}}}\,dr\,}$

${\displaystyle {\frac {v(t)^{2}}{2}}-{\frac {v_{0}^{2}}{2}}={\frac {GM}{r(t)}}-{\frac {GM}{r_{0}}}\,}$

Since we desire escape velocity

${\displaystyle t\rightarrow \infty \ \ r(t)\rightarrow \infty }$ and ${\displaystyle v(t)\rightarrow 0}$

${\displaystyle -{\frac {v_{0}^{2}}{2}}=-{\frac {GM}{r_{0}}}\,}$

${\displaystyle v_{0}={\sqrt {\frac {2GM}{r_{0}}}}\,}$

5 ₀ is the escape velocity and r ₀ is the radius of the planet. Notation that the higher up derivation relies on the equivalence of inertial mass and gravitational mass.

The derivations are consistent

The gravitational acceleration can be obtained from the gravitational constant G and the mass of Earth Thousand:

${\displaystyle k={\frac {GM}{r^{2}}},}$

where r is the radius of Earth. Thus

${\displaystyle five={\sqrt {2gr\,}}={\sqrt {{\frac {2GMr}{r^{two}}}\,}}={\sqrt {{\frac {2GM}{r}}\,}},}$

so the two derivations given above are consequent.

Multiple sources

The escape velocity from a position in a field with multiple sources is derived from the total potential energy per kg at that position, relative to infinity. The potential energies for all sources can simply be added. For the escape velocity this results in the square root of the sum of the squares of the escape velocities of all sources separately.

For instance, at the Earth'due south surface the escape velocity for the combination Earth and Sun is ${\displaystyle \scriptstyle {\sqrt {xi.2^{2}\ +\ 42.one^{2}}}\ =\ 43.56\ \mathrm {km} /\mathrm {s} }$ . Every bit a issue, to leave the solar system requires a speed of 13.6 km/s relative to World in the direction of the Earth's orbital motility, since the speed is then added to the speed of xxx km/due south of that orbital motion

Gravity well

In the hypothetical case of uniform density, the velocity that an object would achieve when dropped in a hypothetical vacuum hole from the surface of the Earth to the center of the Earth is the escape velocity divided by ${\displaystyle \scriptstyle {\sqrt {ii}}}$ , that is, the speed in a circular orbit at a low pinnacle. Correspondingly, the escape velocity from the centre of the Earth would exist ${\displaystyle \scriptstyle {\sqrt {one.5}}}$ times that from the surface.

A refined calculation would take into account the fact that the Globe'south mass is not uniformly distributed every bit the center is approached. This gives college speeds.

Come across too

• Black hole
• Energy
• Gravity
• Rocket

Notes

1. ↑ ^{one.0 ane.i} Georgia State University, Data of Planets. Retrieved Oct xvi, 2008.
2. ↑ Bate, Mueller, and White, 1971, 35.

References

ISBN links support NWE through referral fees

• Bate, Roger R., Donald D. Mueller, and Jerry Eastward. White. Fundamentals of Astrodynamics. New York: Dover Publications, 1971. ISBN 0486600610.
• Schutz, Bernard F. Gravity from the Ground Upward. Cambridge: Cambridge Academy Press, 2003. ISBN 0521455065.
• Vallado, David Anthony, and Wayne D. McClain. Fundamentals of Astrodynamics and Applications. Space Engineering Library, 12. Microcosm, Inc, 2001. ISBN 1881883124.

External links

All links retrieved August 16, 2017.

• Escape velocity: Calculated from mass and distance.
• What is escape velocity?

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides past terms of the Creative Commons CC-by-sa 3.0 License (CC-past-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that tin can reference both the New Earth Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is attainable to researchers here:

• Escape velocity ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Escape velocity"

Annotation: Some restrictions may utilize to utilize of private images which are separately licensed.

filerdoeste.blogspot.com

Source: https://www.newworldencyclopedia.org/entry/Escape_velocity

Share this post